Версія за 18:35, 12 січня 2013

Назва навчальної теми

Линейные функции

Основний та другорядні (дотичні) навчальні предмети

Алгебра (информатика, физика, статистика)

Вік учнів, клас

12-13 лет, 7 класс

Стислий опис проекту (скопіювати з Плану)

Линейная функция

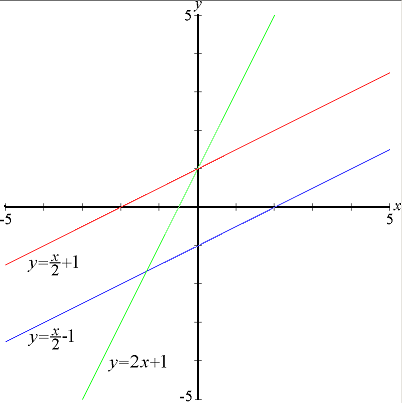
Линейная функция — функция вида у = kx + b(для функций одной переменной).Основное свойство линейных функций: приращение функции пропорционально приращению аргумента. То есть функция является обобщением прямой пропорциональности.График линейной функции является прямой линией, с чем и связано ее название. Это касается вещественной функции одной вещественной переменной.

Примеры линейных функций

Свойства

- является тангенсом угла, который образует прямая с положительным направлением оси абсцисс.

-При , прямая образует острый угол с осью абсцисс.

-При , прямая образует тупой угол с осью абсцисс.

-При , прямая параллельна оси абсцисс.

- является показателем ординаты точки пересечения прямой с осью ординат.

-При , прямая проходит через начало координат.

Линейная функция нескольких переменных

Линейная функция переменных — функция вида

где — некоторые фиксированные числа. Областью определения линейной функции является всё -мерное пространство переменных вещественных или комплексных. При линейная функция называется однородной, или линейной формой.

Если все переменные и коэффициенты — вещественные числа, то графиком линейной функции в -мерном пространстве переменных является -мерная гиперплоскость

в частности при — прямая линия на плоскости.

План вивчення теми (вставити файл)

Оцінювання (стислий опис і інструменти)

Діяльність учнів та вчителя (скопіювати з Плану з посиланнями на відповідні документи)

Відомості про автора

Ім'я, прізвище

Фах, навчальний предмет

Навчальний заклад

Місто\село, район, область

Контактні дані

Відомості про тренінг

Дати проведення тренінгу

Місце проведення тренінгу

МПЛ №125 "Престиж"

Тренери

Ивасенко Лариса Ивановна