Взаємне розміщення прямих на площині-геометрія 7 клас

Дослідження провели

Учні 7 класу

Основна ідея дослідження

Ознайомитись з основними поняттями теми та застосовувати їх при вивченні геометрії

Аксіома

• Твердження, яке приймається без доведення називають аксіомою

Теорема

• Твердження,яке потребує доведення називають теоремою

Доведення

• Доведення або доказ у математиці — процедура, за допомогою якої встановлюють істинність гіпотези чи будь-якого твердження.

Принципи доведення вивчаються спеціальною областю математики — теорією доказів.

Суміжні кути

• Два кути називаються суміжними, якщо в них одна сторона спільна, а інші сторони є доповняльними півпрямими.

на малюнку кути AOC i COB-суміжні.

сторона ОС-спільна

сторони ОА і ОВ є доповняльними півпрямими.

Властивості суміжних кутів

• Теорема 1. Сума суміжних кутів дорівнює 180 градусів. (Зверніть увагу: кути, сума яких дорівнює 180 градусів, не обов’язково суміжні.)

• Теорема 2. Коли два кути рівні, то суміжні з ними кути теж рівні.

• Теорема 3. Кут, суміжний із прямим ­кутом, є прямий кут.

• Теорема 4. Кут, суміжний із гострим ­кутом, — тупий.

• Теорема 5. Кут, суміжний із тупим кутом, — гострий.

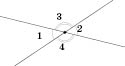
Вертикальні кути

• Два кути називаються вертикальними, якщо сторони одного кута є доповняльними півпрямими сторін другого.

кут 1 та 2-вертикальні

кут 3 та 4-вертикальні

Властивості вертикальних кутів

• Теорема 1. Вертикальні кути рівні.(Але не всі рівні кути вертикальні.)

• Теорема 2. Кути, вертикальні рівним, ­рівні.

• Якщо дві прямі перетинаються, то вони утворюють чотири нерозгорнутих кути. Кожні два із цих кутів або суміжні, або вертикальні:

Паралельні прямі

Паралельними (рівнобіжними) прямими називають прямі, котрі лежать в одній площині і або збігаються, або не перетинаються.

Властивості

• Паралельність — Бінарне відношення еквівалентності, тому разбиває всю множину прямих на класи паралельних між собою.

• Через довільну точку можна провести лише одну пряму, паралельную даній. Це властивість евклідової геометрії, в інших геометріях число 1 замінено іншими (в геометрії Лобачевского таких прямих минімум дві).

• Дві паралельні прямі в просторі лежать в одній площині.

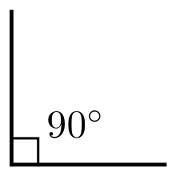
Перпендикулярні прямі

Дві прямі на площині називаються перпендикулярними, якщо при перетині вони утворють 4 прямих кути. Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.

Властивості

• Через точку, що не належить прямій, можна провести пряму, перпендикулярну даній прямій, і тільки одну.

• Відрізки або промені, які лежать на перпендикулярних прямих, називаються перпендикулярними.

• Перпендикуляром до даної прямої називається відрізок прямої, перпендикулярний до даної, який має одним зі своїх кінців точку перетину прямої і відрізка. При цьому кінець відрізка, який лежить на прямій, називається основою перпендикуляра.

• Через кожну точку прямої можна провести перпендикулярну їй пряму й тільки одну.

• З будь-якої точки, що не лежить на даній прямій, можна опустити на цю пряму перпендикуляр і тільки один.

• Довжина перпендикуляра, опущеного з точки на пряму, називається відстанню від точки до прямої.

• Відстань від будь-якої точки однієї з паралельних прямих до другої прямої називається відстанню між паралельними прямими.

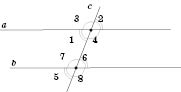
Січна

На рисунку зображені кути, утворені в результаті перетину двох прямих січною:

Пряма, яка перетинає дві задані прямі, називається січною цих прямих.

При перетині прямих січною утворюються такі пари кутів:

• кути, що лежать між прямими і по один бік від січної, називаються внутрішніми односторонніми кутами; маємо дві пари внутрішніх односторонніх кутів;

• кути, що лежать між прямими і по різні боки від січної, називаються внутрішніми різносторонніми кутами; маємо дві пари внутрішніх різносторонніх кутів;

• кути, що лежать по один бік від січної, але один із них лежить між заданими прямими, а інший не лежить між ними, називаються відповідними; маємо чотири пари відповідних кутів.

При перетині двох паралельних прямих січною утворюються кути, що мають такі властивості:

• внутрішні різносторонні кути при паралельних прямих і січній рівні;

• сума двох внутрішніх односторонніх кутів при паралельних прямих і січній дорівнює 180 градусам;

• дві відповідні кути при паралельних прямих і січній рівні.