Користувач:UkhovaElena25
Зміст
- 1 Назва проекту
- 2 Автор проекту
- 3 Клас та вік учнів, які бруть участь у проекті
- 4 Перелік шкільних навчальних предметів
- 5 Час проведення
- 6 Мета проекту
- 7 Опис проекту
- 8 Блог проекту
- 9 Матеріали проекту:
- 9.1 План роботи над проектом
- 9.2 План реалізації проекту
- 9.3 Організаційна схема роботи над проектом
- 9.4 Вчительська презентація
- 9.5 Публікації проекту
- 9.6 Учнівська презентація
- 9.7 Сайт
- 9.8 Тести, опитувальники
- 9.9 Діаграми
- 9.10 Запрошення на захід
- 9.11 Грамота за учать у проекті
- 9.12 Оцінювання роботи учнів
- 10 Використані джерела
- 11 Проекти подібної тематики
- 12 Відгуки про проект
Назва проекту
«Передбачувана випадковість»
Автор проекту
Студентка Криворізького педагогічного інституту фізико-математичного факультету Ухова Олена Михайлівна
Клас та вік учнів, які бруть участь у проекті
11 класс, 16-17 років
Перелік шкільних навчальних предметів
Математика
Інформатика
Природознавство
Біологія
Історія
Час проведення
Березень-квітень 2014 року
Мета проекту
Відкриття учнями "Закону великих чисел"
Опис проекту
Проект охоплює курс теорії ймовірностей, що вивчається у школі. Перед учнями ставляться практичні завдання, які підкріплюються теорією. Працюють 5 груп учнів. Одна з них «Знайки» — вивчають теоретичні основи закону великих чисел та історію виникнення цього розділу та теорії ймовірностей загалом, інші чотири — практично перевірять дію закону великих чисел у різних життєвих ситуаціях – дослідах. «Гравці» розглянуть задачу по наймовірніше число випадання очок на гранях кубиків, лінгвісти познайомлять з задачею «про слова», флористи перевірять чи всходе насіння, та на завершення «Спец-агенти» розкриють тайни «секретного» методу Монте-Карло.
Основні питання:
Ключове питання:
Чи можеш ти передбачити майбутнє?
Тематичне питання:
Чи залежить від випадку результат, на який діє велика кількість випадкових факторів? Яке сума цифр на двох гральних кубиках буде випадати найчастіше? Чи діє закон Бернуллі на практиці? Які можна навести приклади? Як перевірити дію розподілу Бернуллі на практиці? Чи можна точно дізнатися скільки насіння зійде з партії? Чи можна обчислити число пи експериментально?
Змістовні питання:
У чому полягає суть закону Бернуллі? Що таке відносна частота? Як вона обчислюється? У чому суть правил додавання і добутку? Що собою представляє число пи? Як обчислюється число пи?
Навчальні цілі та очікувані результати навчання
Розглянути приклади «дії закону великих чисел»; відкрити закон великих чисел; зробити висновки щодо використання закону великих чисел.
Діяльність учнів. Що повинні зробити?
Зробити припущення, що випадкова величина перестає бути випадковою за умови великої кількості незалежних випробувань; практично перевірити гіпотезу; зробити висновки щодо «дії закону великих чисел» та теоретично обґрунтувати припущення.
Які програмні засоби та технології були використані у роботі на проектом?
Microsoft Office, хмарні технології Google
Блог проекту
Матеріали проекту:
План роботи над проектом
План реалізації проекту
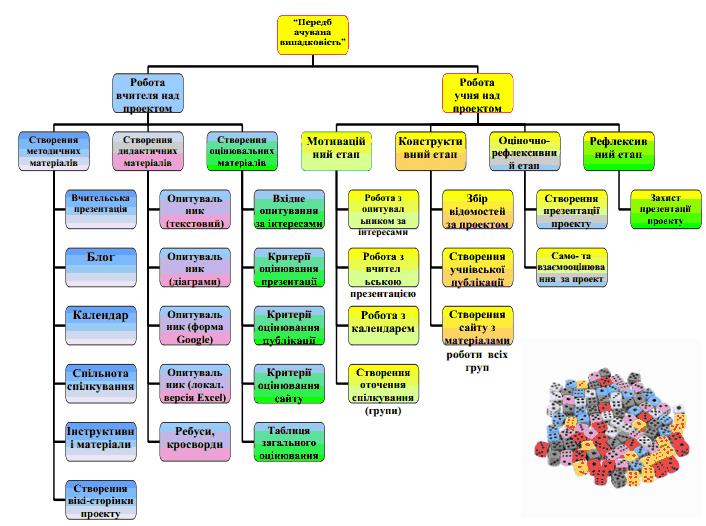
Організаційна схема роботи над проектом
організаційна схема(скачати)
Вчительська презентація
Вчительська презентація - завдання учням
Публікації проекту
Учнівська презентація
Сайт
Тести, опитувальники
опитувальник за інтересами опитувальник за інтересами на сайті
опитувальник з теми (початкового розуміння)
тест в Excel(скачати)
Діаграми
діаграма 2(скачати)
Запрошення на захід
запрошення(використано шаблон Microsoft Publisher)
Грамота за учать у проекті
грамота(використано шаблон Microsoft Publisher)
Оцінювання роботи учнів
Оцінювання учнівської презентації
Оцінювання учнівської публікації
Використані джерела
Бобик О. І. Теорія ймовірностей і математична статистика : підручник / О. І. Бобик, Г. І. Берегова, Б. І. Копитко. – К. : ВД «Професіонал», 2007. – 560с.
Вікіпедія - вільна бібліотека: [1]
Гнеденко Б. В. Курс теории вероятностей: Учебник / Б. В. Гнеденко. – М. : Едиториал УРСС, 2005. – 448с.
Сайт “Факультет пищевых и химических производств АлтГТУ” - [2]
Проекти подібної тематики
Портфоліо Пірус Тетяни з теми "Випадкові події. Теорія ймовірностей"