Відмінності між версіями «Учнівська вікі-стаття "Досліджуємо можливості аркуша в клітинку"»
Gls (обговорення • внесок) (→Полезные ресурсы) |
Gls (обговорення • внесок) (→Полезные ресурсы) |
||
| Рядок 76: | Рядок 76: | ||
==Полезные ресурсы== | ==Полезные ресурсы== | ||
| − | + | Означення прямокутного трикутника [http://uk.wikipedia.org/wiki/%D0%A2%D1%80%D0%B8%D0%BA%D1%83%D1%82%D0%BD%D0%B8%D0%BA] | |
| − | [http://uk.wikipedia.org/wiki/%D0%A2%D1%80%D0%B8%D0%BA%D1%83%D1%82%D0%BD%D0%B8%D0%BA] | + | |
== Другие документы == | == Другие документы == | ||
Версія за 19:03, 3 квітня 2011
Зміст
Назва проекту
Чотирикутники навколо нас
Автори проекту
Голодюк Лариса Степанівна
Тема дослідження
Досліджуємо можливості аркуша у клітинку
Проблемный вопрос (вопрос для исследования)
Як теоретичні знання допомагають на практиці?
Гипотеза исследования
Ми припускаємо, що у зошиті з клітинками можна виконувати точні побудови рисунків до задач.
Цели исследования
Метою нашого дослідження – з’ясувати можливості аркушу в клітинку та подати на обговорення алгоритми побудови чотирикутників.
Результаты исследования
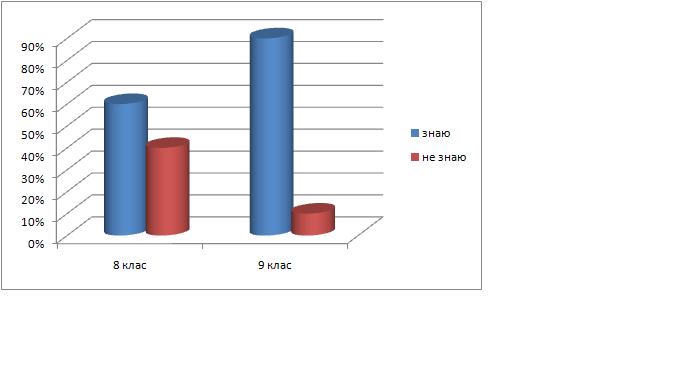
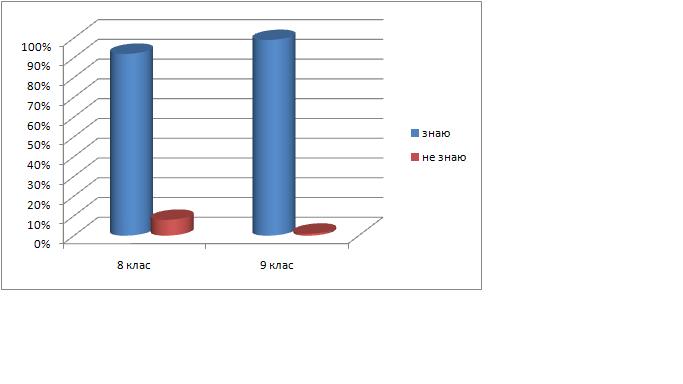
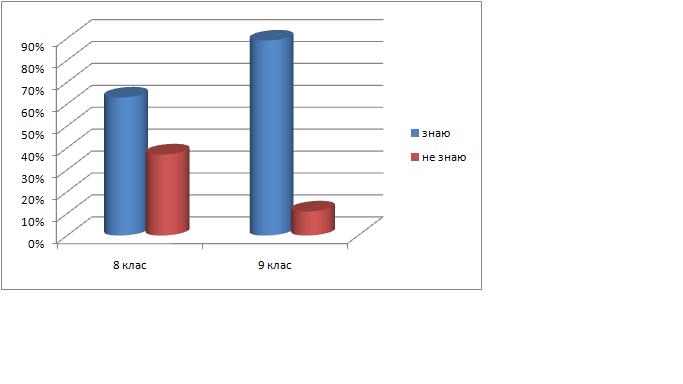
Відомо, що правильно побудований рисунок до задачі – це 80 відсотків розв’язання. Ми дослідили, чи можуть наші ровесники побудувати точний рисунок до задачі за поданими розмірами. Протягом двох днів ми проводили опитування учнів 8 та 9 класів з питання «Які властивості клітинки у зошиті з геометрії ти використовуєш під час побудови рисунка до задачі?». Обробивши результати опитування, ми дійшли висновку, що учні нашої школи знають:
Як побудувати квадрат.
Клітинка має форму квадрата із стороною 0,5 см.
Як побудувати кут, градусна міра якого дорівнює 90 градусів.
Як побудувати кут, градусна міра якого дорівнює 45 градусів.
Провівши конкурсне змагання розв’язування задач на побудову між учнями 8 і 9 класів з’ясувалося, що труднощі виникли під час розв’язування задач під номером 4, 6.
Зроби креслення до задачі на аркуші у клітинку. Побудуй: 1. Квадрат зі стороною 2,5 см. 2. Прямокутну трапецію із основами 3 і 5 см. 3. Ромб із стороною у 5 см. 4. Паралелограм із гострим внутрішнім кутом 45 градусів. 5. Рівнобічну трапецію із тупим внутрішнім кутом 135 градусів. 6. Паралелограм, якщо бісектриса кута перетинає його сторону під кутом 45 градусів. 7. Паралелограм через три точки, що не лежать на одній прямій. Скільки можна побудувати паралелограмів з вершинами у цих точках?
Вывод
У зошиті в клітинку кожна виконувати точні рисунки до задач не використовуючи креслярських інструментів. Для розв’язання запропонованих задач, необхідно було згадати:
• Означення квадрата.
• Означення трапеції та властивість рівнобічної трапеції.
• Означення висоти трапеції.
• Означення ромба.
• Властивість діагоналей ромба.
• Означення паралелограма.
• Властивості сторін паралелограма.
• Означення прямокутника.
• Властивості прямокутника. Слід звернути увагу на розв’язування задачі під номером 3. У процесі її розв’язуванні необхідно скористатися визначенням прямокутного трикутника та властивістю піфагорових трійок, а саме, 3,4,5.
Полезные ресурсы
Означення прямокутного трикутника [1]