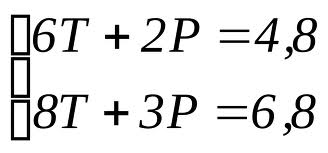Відмінності між версіями «Учнівська Вікі-стаття "Скільки розв'язків має система рівнянь"»
(→Висновки) |
(→Результати дослідження) |
||
| Рядок 35: | Рядок 35: | ||
2. Система має безліч розв'язків, якщо відношення коефіцієнтів при невідомих рівні між собою і дорівнює відношенню вільних членів | 2. Система має безліч розв'язків, якщо відношення коефіцієнтів при невідомих рівні між собою і дорівнює відношенню вільних членів | ||
| − | 3. Система лінійних рівнянь не має жодного розв'язку, якщо відношення коефіцієнтів рівні між собою і не дорівнює відношенню вільних членів | + | 3. Система лінійних рівнянь не має жодного розв'язку, якщо відношення коефіцієнтів рівні між собою і не дорівнює відношенню вільних членів. |
| + | |||
| + | [[Файл:matem.jpg]] | ||
==Висновки== | ==Висновки== | ||
Версія за 15:40, 10 вересня 2012
Зміст
Назва проекту
"Скільки розв'язків має система рівнянь"
Автори проекту
Ткаченко Людмила Леонідівна
Тема дослідження
Навчити учнів досліджувати систему рівнянь і визначати, не розв'язуючи систему, скільки вона має розв'язків
Проблема дослідження
Скільки розв'язків може мати система лінійних рівнянь
Гіпотеза дослідження
Для кожної системи лінійних рівнянь можна сказати: вона має один розв'язок, безліч розв'язків, не мати зовсім розв'язків
Мета дослідження
Навчити учнів самостійно досліджувати систему лінійних рівнянь, щоб сказати скільки вона має розв'язків; готувати учнів до зовнішнього незалежного оцінювання, де використовується даний матеріал
Результати дослідження
1. Система лінійних рівнянь має один розв'язок, якщо коефіцієнти при невідомих не є пропорційними числами
2. Система має безліч розв'язків, якщо відношення коефіцієнтів при невідомих рівні між собою і дорівнює відношенню вільних членів
3. Система лінійних рівнянь не має жодного розв'язку, якщо відношення коефіцієнтів рівні між собою і не дорівнює відношенню вільних членів.
Висновки
Отже, система лінійних рівнянь може мати один розв'язок, безліч розв'язків або зовсім не має розв'язків