Відмінності між версіями «Учнівська вікі--стаття»
(→Результати дослідження) |
|||
| (не показано 26 проміжних версій цього учасника) | |||
| Рядок 1: | Рядок 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Тема дослідження== | ==Тема дослідження== | ||
| + | Три великих задачі старовини | ||
==Проблема дослідження== | ==Проблема дослідження== | ||
| + | Застосування історичних задач на уроках математики | ||
==Гіпотеза дослідження== | ==Гіпотеза дослідження== | ||
| + | Чи можна розвязати дані задачі за допомогою циркуля і лінійки ? | ||
==Мета дослідження== | ==Мета дослідження== | ||
| + | Дослідити розвиток математичних знань древнього світу | ||
==Результати дослідження== | ==Результати дослідження== | ||
| Рядок 19: | Рядок 18: | ||
У XIX столітті було доведено, що всі три задачі нерозв'язні циркулем та лінійкою. Питання можливості побудови повністю вирішене алгебраїчними методами, основаними на теорії Галуа. | У XIX столітті було доведено, що всі три задачі нерозв'язні циркулем та лінійкою. Питання можливості побудови повністю вирішене алгебраїчними методами, основаними на теорії Галуа. | ||
Таким чином, ці задачі виявилися розв'язними за допомогою інших, більше сильних аналітичних засобів. Але їхня значимість у математиці й у науці велика, вони суттєво вплинули на подальший розвиток багатьох розділів математики. Суперечливість і неможливість доведення за допомогою одних засобів і можливість розв'язання їх за допомогою інших, сильніших, виявилося потужним поштовхом у розвитку математики, її основ і філософії. | Таким чином, ці задачі виявилися розв'язними за допомогою інших, більше сильних аналітичних засобів. Але їхня значимість у математиці й у науці велика, вони суттєво вплинули на подальший розвиток багатьох розділів математики. Суперечливість і неможливість доведення за допомогою одних засобів і можливість розв'язання їх за допомогою інших, сильніших, виявилося потужним поштовхом у розвитку математики, її основ і філософії. | ||
| − | Квадратура круга | + | |
| − | + | '''Квадратура круга''' | |
| + | |||
| + | [[Файл:190.jpg|200px|thumb|left|квадратура круга]] | ||
| + | |||
| + | |||
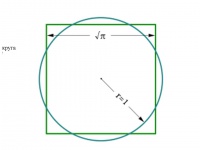
Круг і квадрат однакової площі | Круг і квадрат однакової площі | ||
| Рядок 26: | Рядок 29: | ||
Поруч із трисекцією кута та подвоєнням куба, є однією із найвідоміших задач, що неможливо розв'язати за допомогою циркуля та лінійки. | Поруч із трисекцією кута та подвоєнням куба, є однією із найвідоміших задач, що неможливо розв'язати за допомогою циркуля та лінійки. | ||
| − | Нерозв'язність | + | '''Нерозв'язність''' |
| + | |||
Якщо прийняти за одиницю вимірювання радіус кола і позначити x довжину сторони шуканого квадрата, то задача зводиться до розв'язання рівняння: , звідки: . Як відомо, за допомогою циркуля та лінійки можливо виконати всі 4 арифметичні дії та видобуток квадратного кореня; звідси виходить, що квадратура круга можлива тоді і тільки тоді, коли за допомогою кінцевого числа таких дій можна побудувати відрізок довжини . Таким чином, нерозв'язність цієї задачі витікає з неалгебричності (трансцендентності) числа , яка була доведена в 1882 Ліндеманном. | Якщо прийняти за одиницю вимірювання радіус кола і позначити x довжину сторони шуканого квадрата, то задача зводиться до розв'язання рівняння: , звідки: . Як відомо, за допомогою циркуля та лінійки можливо виконати всі 4 арифметичні дії та видобуток квадратного кореня; звідси виходить, що квадратура круга можлива тоді і тільки тоді, коли за допомогою кінцевого числа таких дій можна побудувати відрізок довжини . Таким чином, нерозв'язність цієї задачі витікає з неалгебричності (трансцендентності) числа , яка була доведена в 1882 Ліндеманном. | ||
Однак цю нерозв'язність слід розуміти, як нерозв'язність при використанні тільки циркуля та лінійки. Задача стає розв'язною, якщо, крім циркуля та лінійки, використовувати інші засоби (наприклад, квадратрису). | Однак цю нерозв'язність слід розуміти, як нерозв'язність при використанні тільки циркуля та лінійки. Задача стає розв'язною, якщо, крім циркуля та лінійки, використовувати інші засоби (наприклад, квадратрису). | ||
| − | Приблизний розв'язок | + | |
| + | '''Приблизний розв'язок''' | ||
| + | |||
В дане коло вписується квадрат. До потроєного діаметру кола додається п'ята частина сторони цього квадрата. Довжина відрізка відрізняється від довжини кола менше ніж на . | В дане коло вписується квадрат. До потроєного діаметру кола додається п'ята частина сторони цього квадрата. Довжина відрізка відрізняється від довжини кола менше ніж на . | ||
Метафора «Квадратура круга» | Метафора «Квадратура круга» | ||
| Рядок 37: | Рядок 43: | ||
Подвоєння куба - класична антична задача на побудову циркулем та лінійкою ребра куба, об'єм якого вдвічі більший за об'єм заданого куба. | Подвоєння куба - класична антична задача на побудову циркулем та лінійкою ребра куба, об'єм якого вдвічі більший за об'єм заданого куба. | ||
Разом з трисекцією кута та квадратурою круга, є однією з найвідоміших нерозв'язних задач на побудову за допомогою циркуля та лінійки. | Разом з трисекцією кута та квадратурою круга, є однією з найвідоміших нерозв'язних задач на побудову за допомогою циркуля та лінійки. | ||
| − | Легенда | + | |
| + | '''Легенда''' | ||
| + | |||
Згідно з античною легендою, одного разу на острові Делос почалася епідемія чуми. Мешканці острова звернулись до дельфійського оракула, і той повідомив, що необхідно подвоїти жертовне святилище, яке мало форму куба. Мешканці Делоса спорудили ще один такий же куб та поставили його на перший, але епідемія не припинилася. Після повторного звернення оракул роз'яснив, що подвоєний жертовник також повинен мати форму куба. | Згідно з античною легендою, одного разу на острові Делос почалася епідемія чуми. Мешканці острова звернулись до дельфійського оракула, і той повідомив, що необхідно подвоїти жертовне святилище, яке мало форму куба. Мешканці Делоса спорудили ще один такий же куб та поставили його на перший, але епідемія не припинилася. Після повторного звернення оракул роз'яснив, що подвоєний жертовник також повинен мати форму куба. | ||
З того часу дельфійською задачею займались найкращі математики античного світу, було запропоновано декілька розв'язків, але ніхто не зміг виконати таку побудову, використовуючи тільки циркуль та лінійку. | З того часу дельфійською задачею займались найкращі математики античного світу, було запропоновано декілька розв'язків, але ніхто не зміг виконати таку побудову, використовуючи тільки циркуль та лінійку. | ||
| − | Спроби розв'язку | + | |
| − | • Гіппократ Хіоський (кінець V ст. до н. е.) показав, що задача зводиться до знаходження двох середніх пропорційних між одним відрізком та іншим, вдвічі більшим за нього. У сучасних позначеннях - до знаходження та таких, що | + | '''Спроби розв'язку''' |
| − | + | ||
| + | :::• Гіппократ Хіоський (кінець V ст. до н. е.) показав, що задача зводиться до знаходження двох середніх пропорційних між одним відрізком та іншим, вдвічі більшим за нього. У сучасних позначеннях - до знаходження та таких, що | ||
| + | Звідси . | ||
• Архіт Тарентський (початок IV ст. до н. е.) запропонував розв'язок, заснований на перетині тора, конуса та кругового циліндра. | • Архіт Тарентський (початок IV ст. до н. е.) запропонував розв'язок, заснований на перетині тора, конуса та кругового циліндра. | ||
• Платон (перша половина IV ст. до н. е.) запропонував механічний розв'язок, заснований на побудові трьох прямокутних трикутників з потрібним співвідношенням сторін. | • Платон (перша половина IV ст. до н. е.) запропонував механічний розв'язок, заснований на побудові трьох прямокутних трикутників з потрібним співвідношенням сторін. | ||
| Рядок 54: | Рядок 64: | ||
У сучасних позначеннях, задача зводиться до розв'язку рівняння . Розв'язок має вигляд . Все зводиться до проблеми побудови відрізка довжиною . | У сучасних позначеннях, задача зводиться до розв'язку рівняння . Розв'язок має вигляд . Все зводиться до проблеми побудови відрізка довжиною . | ||
Ванцель довів у 1837 році, що ця задача не може бути розв'язана за допомогою циркуля та лінійки. | Ванцель довів у 1837 році, що ця задача не може бути розв'язана за допомогою циркуля та лінійки. | ||
| − | Трисекція кута. | + | |
| − | Неперевірена версія | + | '''Трисекція кута.''' |
| + | |||
| + | '''Неперевірена версія''' | ||
Трисекція кута — задача про поділ заданого кута на три рівні частини за допомогою циркуля та лінійки. Інакше кажучи, необхідно побудувати трисектриси кута — промені, що ділять кут на три рівні частини. | Трисекція кута — задача про поділ заданого кута на три рівні частини за допомогою циркуля та лінійки. Інакше кажучи, необхідно побудувати трисектриси кута — промені, що ділять кут на три рівні частини. | ||
Поруч із задачами про квадратуру круга та подвоєння куба є однією з класичних задач на побудову, відомих з часів стародавньої Греції. | Поруч із задачами про квадратуру круга та подвоєння куба є однією з класичних задач на побудову, відомих з часів стародавньої Греції. | ||
П'єр Лоран Ванцель у 1837 році довів, що задача розв'язна тільки тоді, коли розв'язне в квадратних радикалах рівняння: | П'єр Лоран Ванцель у 1837 році довів, що задача розв'язна тільки тоді, коли розв'язне в квадратних радикалах рівняння: | ||
| − | Наприклад, трисекція здійсненна для кутів α = 360°/n при умові, що ціле n не ділиться на 3. Тим не менш, в пресі час від часу публікуються (хибні) способи здійснення трисекції кута циркулем та лінійкою. | + | Наприклад, трисекція здійсненна для кутів α = 360°/n при умові, що ціле n не ділиться на |
| + | |||
| + | 3. Тим не менш, в пресі час від часу публікуються (хибні) способи здійснення трисекції кута циркулем та лінійкою. | ||
Побудова за допомогою додаткових інструментівХоча трисекція кута в загальному випадку нездійсненна за допомогою циркуля і лінійки, існують криві, за допомогою яких цю побудову можна здійснити. Равлик Паскаля або трисектриса, Квадратриса (в давнину також називалась трисектрисою), Конхоїда Нікомеда, Конічні перетини, Спіралі Архімеда. | Побудова за допомогою додаткових інструментівХоча трисекція кута в загальному випадку нездійсненна за допомогою циркуля і лінійки, існують криві, за допомогою яких цю побудову можна здійснити. Равлик Паскаля або трисектриса, Квадратриса (в давнину також називалась трисектрисою), Конхоїда Нікомеда, Конічні перетини, Спіралі Архімеда. | ||
• Трисекция можлива при побудова за допомогою плаского оригамі | • Трисекция можлива при побудова за допомогою плаского оригамі | ||
==Висновки== | ==Висновки== | ||
| + | У XIX столітті було доведено, що всі три задачі нерозв'язні циркулем та лінійкою. Питання можливості побудови повністю вирішене алгебраїчними методами, основаними на теорії Галуа. Таким чином, ці задачі виявилися розв'язними за допомогою інших, більше сильних аналітичних засобів. Але їхня значимість у математиці й у науці велика, вони суттєво вплинули на подальший розвиток багатьох розділів математики. Суперечливість і неможливість доведення за допомогою одних засобів і можливість розв'язання їх за допомогою інших, сильніших, виявилося потужним поштовхом у розвитку математики, її основ і філософії. | ||
==Корисні ресурси== | ==Корисні ресурси== | ||
| + | http://uk.wikipedia.org/wiki/ | ||
Поточна версія на 13:10, 25 лютого 2015
Зміст
Тема дослідження
Три великих задачі старовини
Проблема дослідження
Застосування історичних задач на уроках математики
Гіпотеза дослідження
Чи можна розвязати дані задачі за допомогою циркуля і лінійки ?
Мета дослідження
Дослідити розвиток математичних знань древнього світу
Результати дослідження
Три великі задачі старовини: • 1. Квадратура круга - побудова квадрата, рівновеликого даному кругу (завдання про квадратуру круга), • 2. Подвоєння куба - побудова куба, об′єм якого у два рази перевищує об′єм даного (завдання про подвоєння об'єму куба), • 3. Трисекція кута - розбиття кута на три рівні частини (завдання про трисекцію кута). У XIX столітті було доведено, що всі три задачі нерозв'язні циркулем та лінійкою. Питання можливості побудови повністю вирішене алгебраїчними методами, основаними на теорії Галуа. Таким чином, ці задачі виявилися розв'язними за допомогою інших, більше сильних аналітичних засобів. Але їхня значимість у математиці й у науці велика, вони суттєво вплинули на подальший розвиток багатьох розділів математики. Суперечливість і неможливість доведення за допомогою одних засобів і можливість розв'язання їх за допомогою інших, сильніших, виявилося потужним поштовхом у розвитку математики, її основ і філософії.
Квадратура круга
Круг і квадрат однакової площі Квадратура круга — задача, що полягає в знаходженні побудови за допомогою циркуля та лінійки квадрата, рівновеликого за площею до даного круга. Поруч із трисекцією кута та подвоєнням куба, є однією із найвідоміших задач, що неможливо розв'язати за допомогою циркуля та лінійки.
Нерозв'язність
Якщо прийняти за одиницю вимірювання радіус кола і позначити x довжину сторони шуканого квадрата, то задача зводиться до розв'язання рівняння: , звідки: . Як відомо, за допомогою циркуля та лінійки можливо виконати всі 4 арифметичні дії та видобуток квадратного кореня; звідси виходить, що квадратура круга можлива тоді і тільки тоді, коли за допомогою кінцевого числа таких дій можна побудувати відрізок довжини . Таким чином, нерозв'язність цієї задачі витікає з неалгебричності (трансцендентності) числа , яка була доведена в 1882 Ліндеманном. Однак цю нерозв'язність слід розуміти, як нерозв'язність при використанні тільки циркуля та лінійки. Задача стає розв'язною, якщо, крім циркуля та лінійки, використовувати інші засоби (наприклад, квадратрису).
Приблизний розв'язок
В дане коло вписується квадрат. До потроєного діаметру кола додається п'ята частина сторони цього квадрата. Довжина відрізка відрізняється від довжини кола менше ніж на . Метафора «Квадратура круга» Математичне доведення неможливості квадратури круга не заважало багатьом ентузіастам втрачати роки на розв'язання проблеми. Марність досліджень з розв'язання задачі квадратури круга перенесла цей вираз у багато інших галузей, де він просто позначає безнадійне, безглузде або марне починання. Подвоєння куба Матеріал з Вікіпедії — вільної енциклопедії. Подвоєння куба - класична антична задача на побудову циркулем та лінійкою ребра куба, об'єм якого вдвічі більший за об'єм заданого куба. Разом з трисекцією кута та квадратурою круга, є однією з найвідоміших нерозв'язних задач на побудову за допомогою циркуля та лінійки.
Легенда
Згідно з античною легендою, одного разу на острові Делос почалася епідемія чуми. Мешканці острова звернулись до дельфійського оракула, і той повідомив, що необхідно подвоїти жертовне святилище, яке мало форму куба. Мешканці Делоса спорудили ще один такий же куб та поставили його на перший, але епідемія не припинилася. Після повторного звернення оракул роз'яснив, що подвоєний жертовник також повинен мати форму куба. З того часу дельфійською задачею займались найкращі математики античного світу, було запропоновано декілька розв'язків, але ніхто не зміг виконати таку побудову, використовуючи тільки циркуль та лінійку.
Спроби розв'язку
- • Гіппократ Хіоський (кінець V ст. до н. е.) показав, що задача зводиться до знаходження двох середніх пропорційних між одним відрізком та іншим, вдвічі більшим за нього. У сучасних позначеннях - до знаходження та таких, що
Звідси . • Архіт Тарентський (початок IV ст. до н. е.) запропонував розв'язок, заснований на перетині тора, конуса та кругового циліндра. • Платон (перша половина IV ст. до н. е.) запропонував механічний розв'язок, заснований на побудові трьох прямокутних трикутників з потрібним співвідношенням сторін. • Менехм (середина IV ст. до н. е.) знайшов два розв'язки цієї задачі, засновані на використанні конічних перетинів. У першому розв'язку відшукується точка перетину двох парабол, а у другому - параболи та гіперболи. • Ератосфен (III ст. до н. е.) запропонував ще один розв'язок, в якому використовується спеціальний механічний інструмент - мезолябія, а також описав розв'язок своїх попередників. • Нікомед (II ст. до н. е.) використовував для розв'язку цієї задачі метод вставки, яка виконується за допомогою спеціальної кривої - конхоїди. • Група схожих між собою розв'язків, належачих Аполлонію, Філону Візантійському та Герону, також використовує метод вставки. • У ще одній групі схожих між собою розв'язків, належачих Діоклу, Паппу та Спору, використовується та ж ідея, що і у розв'язку Платона, при цьому Діокл застосовує для побудови спеціальну криву - цисоїду. Свої розв'язки також запропонували Вієт, Декарт, Грегуар де Сен-Венсан, Гюйгенс, Ньютон. Нерозв'язність У сучасних позначеннях, задача зводиться до розв'язку рівняння . Розв'язок має вигляд . Все зводиться до проблеми побудови відрізка довжиною . Ванцель довів у 1837 році, що ця задача не може бути розв'язана за допомогою циркуля та лінійки.
Трисекція кута.
Неперевірена версія Трисекція кута — задача про поділ заданого кута на три рівні частини за допомогою циркуля та лінійки. Інакше кажучи, необхідно побудувати трисектриси кута — промені, що ділять кут на три рівні частини. Поруч із задачами про квадратуру круга та подвоєння куба є однією з класичних задач на побудову, відомих з часів стародавньої Греції. П'єр Лоран Ванцель у 1837 році довів, що задача розв'язна тільки тоді, коли розв'язне в квадратних радикалах рівняння:
Наприклад, трисекція здійсненна для кутів α = 360°/n при умові, що ціле n не ділиться на
3. Тим не менш, в пресі час від часу публікуються (хибні) способи здійснення трисекції кута циркулем та лінійкою. Побудова за допомогою додаткових інструментівХоча трисекція кута в загальному випадку нездійсненна за допомогою циркуля і лінійки, існують криві, за допомогою яких цю побудову можна здійснити. Равлик Паскаля або трисектриса, Квадратриса (в давнину також називалась трисектрисою), Конхоїда Нікомеда, Конічні перетини, Спіралі Архімеда. • Трисекция можлива при побудова за допомогою плаского оригамі
Висновки
У XIX столітті було доведено, що всі три задачі нерозв'язні циркулем та лінійкою. Питання можливості побудови повністю вирішене алгебраїчними методами, основаними на теорії Галуа. Таким чином, ці задачі виявилися розв'язними за допомогою інших, більше сильних аналітичних засобів. Але їхня значимість у математиці й у науці велика, вони суттєво вплинули на подальший розвиток багатьох розділів математики. Суперечливість і неможливість доведення за допомогою одних засобів і можливість розв'язання їх за допомогою інших, сильніших, виявилося потужним поштовхом у розвитку математики, її основ і філософії.