Відмінності між версіями «Графіки тригонометричних функцій в нашому житті»
Матеріал з Iteach WIKI
(→Проблема дослідження) |
(→Корисні ресурси) |
||
| (не показано 27 проміжних версій цього учасника) | |||
| Рядок 3: | Рядок 3: | ||
[[Файл:1359721988_532914753.gif|center]] | [[Файл:1359721988_532914753.gif|center]] | ||
| − | |||
==Автори проекту== | ==Автори проекту== | ||
[[Користувач:Троцька Марія Вікторівна|Троцька Марія]], [[Користувач:Кожушна Катерина|Кожушна Катерина]], [[Користувач:Лавріненко Ольга|Лавріненко Ольга]] - учениці 11-А класу | [[Користувач:Троцька Марія Вікторівна|Троцька Марія]], [[Користувач:Кожушна Катерина|Кожушна Катерина]], [[Користувач:Лавріненко Ольга|Лавріненко Ольга]] - учениці 11-А класу | ||
| − | + | [[Файл:Astroid2.gif|right]] | |
==Тема дослідження== | ==Тема дослідження== | ||
| Рядок 15: | Рядок 14: | ||
==Проблема дослідження== | ==Проблема дослідження== | ||
| − | Визначити | + | Визначити ізнос покришок камер велосипеду в залежності від їх розміру |
==Гіпотеза дослідження== | ==Гіпотеза дослідження== | ||
| + | |||
| + | Астроїда - крок у напрямку до вирішення проблеми | ||
==Мета дослідження== | ==Мета дослідження== | ||
| + | |||
| + | Показати реальний приклад застосування знань з тригонометрії в нашому повсякденному житті | ||
==Результати дослідження== | ==Результати дослідження== | ||
| + | |||
| + | На жаль, поки у авторів проекту не має можливості показати всі розрахунки по розв'язанню системи, її аналізу та побудові її графіку, але основним результатом дослідження є висновок про пряму залежність ізносу покришок камер велосипеду з їх розміром. | ||
| + | |||
| + | Багато корисної використаної інформації можна знайти в розділі '''Корисні ресурси'''. | ||
==Висновки== | ==Висновки== | ||
| + | |||
| + | * В ході нашого дослідження ми познайомилися з історією тригонометрії та розвитком її як невід'ємної частини математики. | ||
| + | |||
| + | * Ми дослідили та проаналізували дану нам систему тригонометричних рівнянь, побудували графік системи - так звану астроїду. | ||
| + | |||
| + | * В ході зміни параметрів системи та оцінки отриманих кожного разу результатів, ми знайшли залежність кількості обертів колес велосипеда з різницею в розмірах цих колес. | ||
| + | |||
| + | * Ми вважаємо, що тригонометрія має широкий спектр застосування в нашому житті. Сфери, в яких вона відіграє важливу роль, постійно розширюються. | ||
==Корисні ресурси== | ==Корисні ресурси== | ||
| + | |||
| + | * [http://kvant.info/panov/kot/kopernik.html/ Котёнок, Коперник и астроида] | ||
| + | |||
| + | * [http://ru.wikipedia.org/wiki/%D0%90%D1%81%D1%82%D1%80%D0%BE%D0%B8%D0%B4%D0%B0/ Астроида] | ||
| + | |||
| + | * [http://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B8%D0%B3%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F/ Тригонометрия] | ||
| + | |||
| + | * [http://matematikam.ru/calculate-online/grafik.php/ Построение графиков онлайн] | ||
Поточна версія на 00:51, 8 лютого 2013
Краса тригонометрії
Зміст
Автори проекту
Троцька Марія, Кожушна Катерина, Лавріненко Ольга - учениці 11-А класу
Тема дослідження
Тригонометрія в нашому житті
Проблема дослідження
Визначити ізнос покришок камер велосипеду в залежності від їх розміру
Гіпотеза дослідження
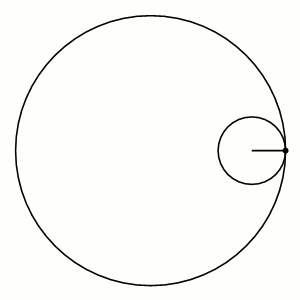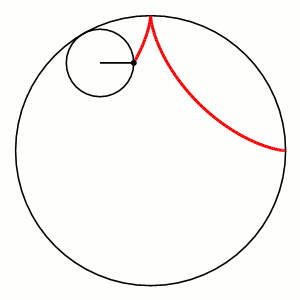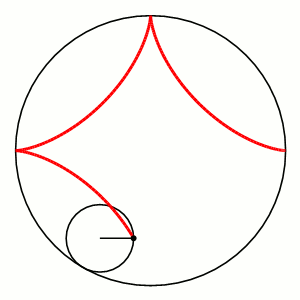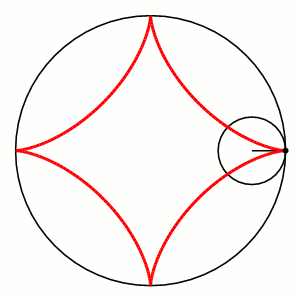
Астроїда - крок у напрямку до вирішення проблеми
Мета дослідження
Показати реальний приклад застосування знань з тригонометрії в нашому повсякденному житті
Результати дослідження
На жаль, поки у авторів проекту не має можливості показати всі розрахунки по розв'язанню системи, її аналізу та побудові її графіку, але основним результатом дослідження є висновок про пряму залежність ізносу покришок камер велосипеду з їх розміром.
Багато корисної використаної інформації можна знайти в розділі Корисні ресурси.
Висновки
- В ході нашого дослідження ми познайомилися з історією тригонометрії та розвитком її як невід'ємної частини математики.
- Ми дослідили та проаналізували дану нам систему тригонометричних рівнянь, побудували графік системи - так звану астроїду.
- В ході зміни параметрів системи та оцінки отриманих кожного разу результатів, ми знайшли залежність кількості обертів колес велосипеда з різницею в розмірах цих колес.
- Ми вважаємо, що тригонометрія має широкий спектр застосування в нашому житті. Сфери, в яких вона відіграє важливу роль, постійно розширюються.