Відмінності між версіями «Проект з математики "Вимірюємо недосяжне"»
(→Діяльність учнів та вчителя (скопіювати з Плану з посиланнями на відповідні документи)) |
(→Діяльність учнів та вчителя (скопіювати з Плану з посиланнями на відповідні документи)) |
||
| Рядок 139: | Рядок 139: | ||
'''Це''' | '''Це''' | ||
[https://docs.google.com/presentation/d/1svlF5gM9fYK7OnSYxo_L5ecktpB2D527lcVDV8xp7iU/edit#slide=id.p14 Презентація групи астродослідників] | [https://docs.google.com/presentation/d/1svlF5gM9fYK7OnSYxo_L5ecktpB2D527lcVDV8xp7iU/edit#slide=id.p14 Презентація групи астродослідників] | ||
| − | [[Файл: | + | |
| + | [[Файл: St3 pr9g.JPG | 600px|thumb|center]]<BR> | ||
'''Презентація групи експертів з DG''' | '''Презентація групи експертів з DG''' | ||
Версія за 20:54, 1 квітня 2013
Зміст
- 1 Назва навчальної теми
- 2 Основний та другорядні (дотичні) навчальні предмети
- 3 Вік учнів, клас
- 4 Стислий опис проекту (скопіювати з Плану)
- 5 План вивчення теми (вставити файл)
- 6 Оцінювання (стислий опис і інструменти)
- 7 Діяльність учнів та вчителя (скопіювати з Плану з посиланнями на відповідні документи)
- 8 Відомості про автора
- 9 Відомості про тренінг
Назва навчальної теми
«Розв’язування трикутників»
Основний та другорядні (дотичні) навчальні предмети
Основний предмет геометрія
Другорядний (дотичний) інформатика
Вік учнів, клас
9 клас, 14-15 років
Стислий опис проекту (скопіювати з Плану)
Проект з геометрії для учнів 9-го класу по темі «Розв’язування трикутників»
Ключове запитання Чи можливо виміряти недосяжне ?
Тематичні запитання
1. Для чого потрібно вивчати теорему синусів та теорему косинусів?
2. Яке практичне застосування теореми синусів та теореми косинусів?
Змістові запитання
1) В чому полягає «розв’язування трикутників»?
2) Скільки елементів трикутника мають бути відомими, щоб його можна було розв’язувати?
3) Які теореми потрібно знати, щоб розв’язати трикутник?
4) Які співвідношення необхідно застосувати для знаходження невідомих елементів трикутника?
Цей проект - практична робота, він включає:
- пошук інформації про історію виникнення та розвиток тригонометрії,
- дослідження галузей застосування на практиці теореми синусів та теореми косинусів при розв’язуванні трикутників.
Учні діляться на три групи:
- «журналісти»,
- «практики» ,
- «дослідники-експерти»
Одна із груп (журналісти) виконує пошук в Інтернеті матеріалу по історії виникнення та становлення тригонометрії і методу розв’язування трикутників.
Свої напрацювання вона подає у вигляді статті-сторінки в Щоденнику Ua на сторінці школи.
Друга група(практики) виконує пошук і розв’язування практичних життєвих прикладних задач, використовуючи матеріали підручників з геометрії та Інтернету і подає свої знахідки у вигляді презентації.
Третя група (дослідники-експерти) проводять дослідження за допомогою програми «Динамічна геометрія», створюючи програму з обчислення невідомих величин за допомогою програми EXCEL та задачі на відстані з астрономії (розглядаючи як плацдарм космічні віддалі та об’єкти).
Учні демонструють свої знання на практичних моделях, у формі мультимедійних презентацій, публікацій та усних виступів В процесі роботи над проектом формують навички критичного мислення, розвивають творчі здібності, вміння спілкуватися та лаконічно подавати свою думку
План вивчення теми (вставити файл)
Оцінювання (стислий опис і інструменти)
Оцінювання відбувається упродовж всього проекту
Для оцінювання роботи учнів вивчення теми використовується:
- Контрольний список для визначення наявності та рівня попередніх знань ( ЗХД )
- Тест сприйняття навчального матеріалу "Так чи ні?"
або різновид 2
Для оцінювання результатів роботи в проекті використана:
Діяльність учнів та вчителя (скопіювати з Плану з посиланнями на відповідні документи)
Крок 1.
- Вчитель пропонує учням переглянути буклет про метод проектів(Word для закачування) ( стор.1 та стор. 2 ) та вступну презентацію до даного проекту,
пройти онлайн тестування для перевірки готовності до проекту і переглянути таблицю «ЗХД» та виконати навчальний тест,
а учні знайомляться із планом вивчення теми і виконують тест.
Крок 2
- Вчитель пропонує учням презентацію "Авторське право" презентацію та лист-дозвіл батьків на публікацію своїх досліджень в Інтернеті
Крок 3.
- Вчитель об’єднує учнів у 4 групи для проведення дослідження за інтересами та результатами тесту.
Попередньо учні знайомляться з критеріями оцінювання презентації та визначають свій рівень творчості за критеріями оцінювання творчості
Утворюються групи
- 1-а група - журналісти ,які збиратимуть матеріал з історії виникнення та розвитку тригонометрії в Інтернеті та книгах та створять презентацію про це
- 2-а група - практики - будуть шукати способи застосування на практиці одержаних знань, зроблять огляд повсякденних практичних задач для обчислення невідомих відрізків, недоступних відстаней
- 3-я група – дослідники-експерти - проведуть дослідження для задач на відстані з астрономії (розглядаючи як плацдарм космічні віддалі та об’єкти у Всесвіті) та застосують у дослідженні програми DG i Excel
Крок 4.
- Учитель пропонує учням загальний план роботи , інструкцію по виконанню проекту .
- Учні знайомляться із запропонованими матеріалами, аналізують сайти за допомогою схеми, яку дає вчитель.
Крок 5.
- Учитель разом з учнями з дозволу батьків створює електронні скриньки для обміну інформацією (якщо ці скриньки ще не були створені раніше) .
Крок 6
- Учитель під час проведення дослідження за графіком проводить консультації для груп учнів.
- Учні беруть участь у консультаціях, задають питання, обговорюють проблеми.
- Учитель розсилає форму для опитування на електронні адреси учнів.
- Учні дають відповіді, які вчитель перевіряє і ставить проміжну оцінку.
З окремими учнями вчитель проводить індивідуальні консультації або є відсилає учням коментарі до завдань і відповідей.
Крок 7.
Виконання проекту
- 1-а група - журналісти розподіляють між собою обов’язки по збору матеріалів, збирають матеріал з Інтернету та книг та створюють [презентацію
- 2-а група - практики – шукають способи застосування на практиці одержаних знань і створюють відповідні схеми розв’язування задач практичного змісту. За результатами роботи створюється презентація-звіт групи практиків
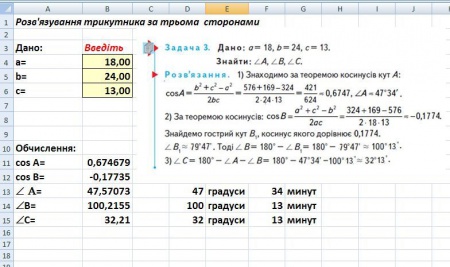
- 3-я група – дослідники-експерти - проводять дослідження за допомогою програми «Динамічна геометрія», створюють програму з обчислення невідомих величин за допомогою програми EXCEL та розбирають задачі на відстані з астрономії (розглядаючи як плацдарм космічні віддалі та об’єкти у Всесвіті). Свої дослідження вони подають у створених програмах в DG, EXCELі та презентації
Крок 8.
- Учні презентують свою роботу усно, демонструючи вікі-сторінки, презентації та створені програми
Це Презентація групи астродослідників
[[Файл: St3 pr9g.JPG | 600px|thumb|center]]
Презентація групи експертів з DG
* звіт DG (малюнок) та * Файл "Розв'язування трикутників" типу DG-файл
* Презентація групи експертів(EXCEL)
* Розв'язування трикутників в Excel та малюнки відповідних сторінок І-ої , 2-ої, 3-ьої, 4-ої
Для проведення диференціації:
- учні можуть обирати, який обсяг матеріалу з цієї області знань вони хотіли б вивчити;
- їм дозволено учням обирати і виконувати альтернативні, рівнозначні завдання до тих, які ставить вчитель;
- учні вчаться за допомогою проектування або побудови моделей (Динамічна геометрія), програмувати в електронних таблицях(поглиблений рівень дослідження) ;
- учням пропонують з метою дослідження різних тем працювати індивідуально та в невеликих групах;
- учні можуть обирати, чи їм працювати самостійно, чи у групі;
- учні об’єднуються в групи в залежності від їх потреб та здібностей.
Відомості про автора
Ім'я, прізвище
Фах, навчальний предмет
Вчитель-методист
Вчитель математики, фізики, інформатики
Навчальний заклад
Зборівська державна українська гімназія ім. Романа Завадовича Тернопільської області
Місто\село, район, область
Місто Зборів Тернопільської області
Контактні дані
e-mail: galina_pan@i.ua
Відомості про тренінг
Дати проведення тренінгу
25-31 березня 2013 року