Відмінності між версіями «Вікі-стаття Історія винекнення теореми Піфагора»
(→Автори проекту) |
(→Результати дослідження) |
||
| (не показано 11 проміжних версій цього учасника) | |||
| Рядок 8: | Рядок 8: | ||
==Тема дослідження== | ==Тема дослідження== | ||
| − | + | Теорема Піфагора | |
==Проблема дослідження== | ==Проблема дослідження== | ||
| + | Історична необхідність теореми Піфагора | ||
==Гіпотеза дослідження== | ==Гіпотеза дослідження== | ||
| − | + | Чи дійсно Піфагор є автором теореми Піфагора? | |
==Мета дослідження== | ==Мета дослідження== | ||
| − | + | Практичне застосування теореми Піфагора | |
==Результати дослідження== | ==Результати дослідження== | ||
| + | |||
| + | [[Файл:Image-11720.gif]] | ||
| + | |||
| + | |||
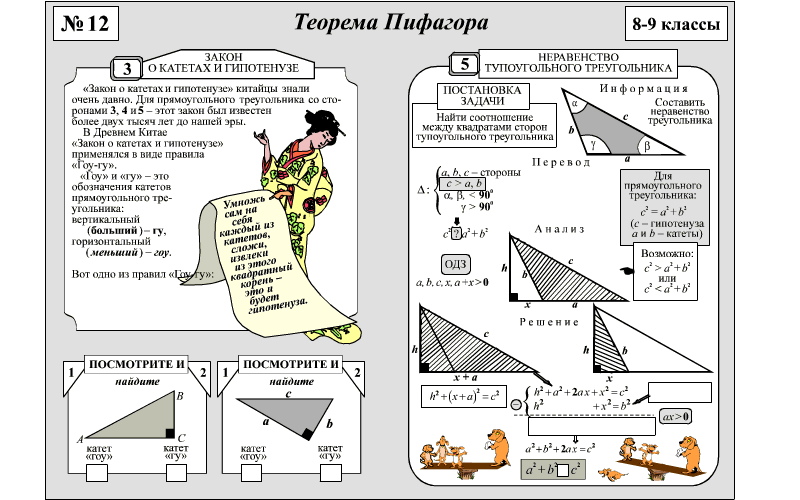
| + | Прямокутні трикутники мають властивість, яка сформульована втеоремі Піфагора: у прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. | ||
| + | Якщо у деякому трикутнику сума квадратів двох сторін дорівнює квадрату третьої сторони, то такий трикутник є прямокутним. | ||
| + | У будь-якому прямокутному трикутнику катет менший від гіпотенузи. | ||
| + | Квадрат катета прямокутного трикутника дорівнює різниці квадрата гіпотенузи і квадрата другого катета. | ||
| + | Окремі випадки Теореми Піфагора, зокрема щодо так званих єгипетських, або «священних», трикутників зі сторонами 3, 4 і 5, були відомі ще до Піфагора в Стародавньому Єгипті, у Вавилоні, Індії і Китаї. Можливо, Піфагор першим навів доведення цієї теореми. | ||
| + | Числа, які можуть бути сторонами прямокутного трикутника, тобто зв’язані залежністю, яку виражає теорема Піфагора, називаютьсячислами Піфагора. Найпростішим прикладом таких чисел є 3, 4 і 5, а також трійки чисел, кратних числам цієї трійки, наприклад, 6, 8 і 10 і так далі. | ||
| + | Є нескінченна множина трійок піфагорових чисел. Відповідні їм трикутники називають єгипетськими. Вважають, що єгипетські землеміри будували прямі кути за допомогою мотузки з 12 вузлами на ній, однаково віддаленими один від одного. Мабуть, тому і самих землемірів називали натягувачами мотузокок. В окремих випадках таким прийомом користуються і сьогодні. | ||
==Висновки== | ==Висновки== | ||
| − | + | Розв'язуючи задачі на прямокутні трикутники обов'язково використовується теорема Піфагора. | |
| + | Також ця терема використовується для доведення, що трикутник прямокутний. | ||
==Корисні ресурси== | ==Корисні ресурси== | ||
| + | http://uk.wikipedia.org | ||
| + | http://shkolyar.in.ua | ||
Поточна версія на 16:40, 1 листопада 2012
Зміст
Назва проекту
Історія винекнення теореми Піфагора
Автори проекту
2 група "Теоретики"
Тема дослідження
Теорема Піфагора
Проблема дослідження
Історична необхідність теореми Піфагора
Гіпотеза дослідження
Чи дійсно Піфагор є автором теореми Піфагора?
Мета дослідження
Практичне застосування теореми Піфагора
Результати дослідження
Прямокутні трикутники мають властивість, яка сформульована втеоремі Піфагора: у прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.
Якщо у деякому трикутнику сума квадратів двох сторін дорівнює квадрату третьої сторони, то такий трикутник є прямокутним.
У будь-якому прямокутному трикутнику катет менший від гіпотенузи.
Квадрат катета прямокутного трикутника дорівнює різниці квадрата гіпотенузи і квадрата другого катета.
Окремі випадки Теореми Піфагора, зокрема щодо так званих єгипетських, або «священних», трикутників зі сторонами 3, 4 і 5, були відомі ще до Піфагора в Стародавньому Єгипті, у Вавилоні, Індії і Китаї. Можливо, Піфагор першим навів доведення цієї теореми.
Числа, які можуть бути сторонами прямокутного трикутника, тобто зв’язані залежністю, яку виражає теорема Піфагора, називаютьсячислами Піфагора. Найпростішим прикладом таких чисел є 3, 4 і 5, а також трійки чисел, кратних числам цієї трійки, наприклад, 6, 8 і 10 і так далі.
Є нескінченна множина трійок піфагорових чисел. Відповідні їм трикутники називають єгипетськими. Вважають, що єгипетські землеміри будували прямі кути за допомогою мотузки з 12 вузлами на ній, однаково віддаленими один від одного. Мабуть, тому і самих землемірів називали натягувачами мотузокок. В окремих випадках таким прийомом користуються і сьогодні.
Висновки
Розв'язуючи задачі на прямокутні трикутники обов'язково використовується теорема Піфагора. Також ця терема використовується для доведення, що трикутник прямокутний.