Відмінності між версіями ««Чим може здивувати «хитрий» многочлен?»»
(Створена сторінка: {{subst:Шаблон:Вікі-стаття учня}}) |
(→Висновки) |
||
| (не показано 8 проміжних версій цього учасника) | |||
| Рядок 5: | Рядок 5: | ||
==Назва проекту== | ==Назва проекту== | ||
| + | Ода цілим виразам | ||
==Автори проекту== | ==Автори проекту== | ||
| + | Сімейко Алла Іванівна | ||
==Тема дослідження== | ==Тема дослідження== | ||
| + | Многочлени, їх запис, дії над многочленами | ||
==Проблема дослідження== | ==Проблема дослідження== | ||
| + | Які математичні записи можна вважати многочленами? | ||
==Гіпотеза дослідження== | ==Гіпотеза дослідження== | ||
| + | Ми вважаємо, що записи (а+b)c та abc можна вважати многочленами? | ||
==Мета дослідження== | ==Мета дослідження== | ||
| + | Дослідити, чи можна вважати записи (а+в)с та (авс) ̅ многочленами, адже вони перетворюються у суми одночленів. | ||
==Результати дослідження== | ==Результати дослідження== | ||
| + | [[Файл:vss1.jpg |1000x300px]] | ||
| + | |||
| + | У математиці часто доводиться додавати чи віднімати од¬ночлени. Наприклад, 7х + 2а — сума, а 7х - 2а — різниця одночленів 7х і 2а. Вираз 7х - 2а можна вважати також сумою одночленів 7х і -2а, бо 7х + (-2а) = 7х - 2а. Вираз 2х4 - Зх3 +х2-9х- 2 — сума одночленів 2х4, -Зх3, х2, -9х і-2. | ||
| + | |||
| + | '''Суму кількох одночленів називають многочленом.''' | ||
| + | Кожний доданок многочлена називається його членом. На¬приклад, многочлен 2ху - 5х + 6 містить три члени: 2ху, -5х і 6. | ||
| + | |||
| + | Якщо многочлен містить два доданки, він називається двочленом, три — тричленом. Одночлен також вважається окремим видом многочлена. | ||
| + | |||
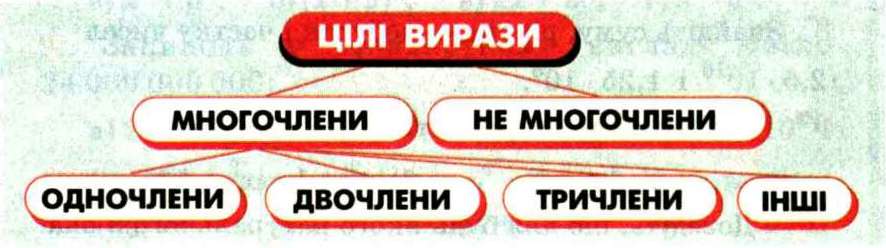
| + | Існують ділі вирази, які не є многочленами. Наприклад, вирази (а - b)2, 2а - (b + х)3 цілі, але не є многочленами. Зв’язки між згадуваними виразами ілюструє малюнок | ||
| + | |||
| + | [[Файл:vss2.jpg|1000x300px]] | ||
| + | |||
| + | Многочлен може мати подібні члени, тобто такі доданки, які відрізняються тільки коефіцієнтами або й зовсім не відрізняються. Наприклад, у тричлені 4х + 9х - 5 перші два. | ||
| + | |||
| + | х3 - 2х2 + 3х + 7, аb + bс-са, 2ax - За • 5х + 8 два перших вирази — многочлени стандартного вигляду, а третій — ні. На основі законів дій кожний много¬член можна подати в стандартному вигляді, наприклад: | ||
| + | 2ах - За * 5х + 8 = 2аx - 15ах + 8 = -13ax + 8. | ||
| + | |||
| + | Члени многочлена можна записувати в різній послідов¬ності. Здебільшого їх упорядковують за спадними показ¬никами тієї чи іншої змінної. Наприклад, упорядкувавши многочлен 5ах2 + 6х3 - 4а2х + а4 за спадними степенями змінної х, одержимо 6х3 + 5ах2 -4ах + а4 . Найвищий по¬казник степеня змінної х дорівнює трьом, тому такий мно¬гочлен називають многочленом третього степеня віднос¬но х. Його можна впорядкувати і за спадними степенями змінної а: а4 - 4а2х + 5ах2 + 6x3 Це многочлен четвертого степеня відносно змінної а. | ||
| + | |||
| + | '''Чи задумувалися ви над таким?''' | ||
| + | Чи є многочленами вирази (а + b)с,(abc)? Іноді відповідають на це запи¬тання ствердно, бо, мовляв, згідно з розподільним законом множен¬ня даний вираз тотожно дорівнює двочленові ас + bс, а отже і він є двочленом. Або, наприклад, запис (abc) (він означає трицифрове число, у якому a сотень, b десятків і c одиниць) перетворюється у тричлен: (abc)= 100a+10b+c . Це неправильно. В алгебрі вирази прийнято називати залежно від того, як вони записані, а не від того, як їх можна записати. | ||
| + | |||
| + | Розглянемо приклад. Вираз 8а можна подати у вигляді суми двох, трьох чи будь-якої іншої кількості доданків: | ||
| + | |||
| + | 8а = За + 5а, 8а = а + За + 4а, 8а=а+а+а+а+4а. | ||
| + | |||
| + | Якщо, виходячи з цього, вираз 8а називати і одночленом, і дво¬членом, і тричленом тощо, то це буде дуже незручно. Тому в алгебрі домовилися вирази називати так, як вони записані, а не так, як їх мож¬на записати, виконавши ті чи інші тотожні перетворення. | ||
| + | |||
| + | (а + b)с — ні одночлен, ні многочлен. Теж саме можна стверджувати і про запис (abc). | ||
| + | А от вираз ∑_0^n▒〖a_i x^i 〗 можна вважати многочленом, бо це скорочений запис многочлена a_0 x^0+a_1 x^1+a_2 x^2+a_3 x^3+a_4 x^4+…+a_n x^n. | ||
| + | |||
| + | '''ДОДАВАННЯ І ВІДНІМАННЯ МНОГОЧЛЕНІВ''' | ||
| + | |||
| + | [[Файл:vss3.jpg|1000x250px]] | ||
| + | |||
| + | Щоб додати два многочлени, тобто знайти суму многочленів, достатньо сполучити їх знаком «плюс». | ||
| + | Наприклад, сумою многочленів а2 + ах + x3 і с2 + сх + х є многочлен а2 + ах + х3 + с2 + сх + х. Якщо в знайденій сумі є подібні члени, їх слід звести. Так само додають три і більше многочленів. | ||
| + | |||
| + | Приклад. Додайте многочлени | ||
| + | х2 + 2х + 4, 3х2 - 4 і 3 - 2х. | ||
| + | Розв’язання. | ||
| + | х2 + 2х + 4 + 3х2 - 4 + 3 - 2х = 4х2 + 3. | ||
| + | Додавання многочленів підпорядковується перестав¬ному і сполучному законам: які б не були многочлени А, В і С, завжди | ||
| + | А + В = В + А і (А + В) + С = А + (B + С). | ||
| + | |||
| + | Щоб знайти різницю двох многочленів, треба від першо¬го з них відняти другий. | ||
| + | Виконуючи таке завдання, після першого многочлена пи¬шуть знак «мінус», а другий беруть у дужки. | ||
| + | Розкриваючи дужки, перед якими стоїть знак «мінус», знаки всіх членів, що були в цих дужках, змінюють на протилежні. | ||
| + | |||
| + | Приклад. Знайдіть різницю многочленів | ||
| + | аb + с - 4 і 2аb + с - 3. | ||
| + | Розв’язання. аb + с - 4- (2 аb + с - 3) = аb + с - 4 - 2аb - с + 3 = -аb - 1. | ||
| + | |||
| + | Отже, і сума, і різниця довільних многочленів — много¬члени. | ||
| + | |||
| + | '''Хочете знати ще більше?''' | ||
| + | |||
| + | Якою може бути сума двох двочленів? Вона може мати кілька | ||
| + | членів, дорівнювати якому-небудь числу, зокрема й нулю. Додайте, на¬приклад, до двочлена 4с - 5х послідовно двочлени с2 + 1, с2 + 5х, 5х-7, 5х - 4с і переконайтеся в цьому. | ||
| + | |||
| + | Оскільки многочленами вважають і одночлени, і будь-які числа, зокре¬ма й нуль, то сума будь-яких многочленів є многочленом. Тому говорять, що в множині многочленів додавання і віднімання завжди можливе. | ||
==Висновки== | ==Висновки== | ||
| + | В алгебрі домовилися вирази називати так, як вони записані, а не так, як їх мож¬на записати, виконавши ті чи інші тотожні перетворення. Тому записи (а+в)с та (авс) ̅ (та інші ) многочленами не вважаються. | ||
| + | |||
| + | [[Файл:vss4.jpg]] | ||
==Корисні ресурси== | ==Корисні ресурси== | ||
[[Категорія: Шаблони]] | [[Категорія: Шаблони]] | ||
Поточна версія на 15:31, 29 вересня 2012
Зміст
Назва проекту
Ода цілим виразам
Автори проекту
Сімейко Алла Іванівна
Тема дослідження
Многочлени, їх запис, дії над многочленами
Проблема дослідження
Які математичні записи можна вважати многочленами?
Гіпотеза дослідження
Ми вважаємо, що записи (а+b)c та abc можна вважати многочленами?
Мета дослідження
Дослідити, чи можна вважати записи (а+в)с та (авс) ̅ многочленами, адже вони перетворюються у суми одночленів.
Результати дослідження
У математиці часто доводиться додавати чи віднімати од¬ночлени. Наприклад, 7х + 2а — сума, а 7х - 2а — різниця одночленів 7х і 2а. Вираз 7х - 2а можна вважати також сумою одночленів 7х і -2а, бо 7х + (-2а) = 7х - 2а. Вираз 2х4 - Зх3 +х2-9х- 2 — сума одночленів 2х4, -Зх3, х2, -9х і-2.
Суму кількох одночленів називають многочленом. Кожний доданок многочлена називається його членом. На¬приклад, многочлен 2ху - 5х + 6 містить три члени: 2ху, -5х і 6.
Якщо многочлен містить два доданки, він називається двочленом, три — тричленом. Одночлен також вважається окремим видом многочлена.
Існують ділі вирази, які не є многочленами. Наприклад, вирази (а - b)2, 2а - (b + х)3 цілі, але не є многочленами. Зв’язки між згадуваними виразами ілюструє малюнок
Многочлен може мати подібні члени, тобто такі доданки, які відрізняються тільки коефіцієнтами або й зовсім не відрізняються. Наприклад, у тричлені 4х + 9х - 5 перші два.
х3 - 2х2 + 3х + 7, аb + bс-са, 2ax - За • 5х + 8 два перших вирази — многочлени стандартного вигляду, а третій — ні. На основі законів дій кожний много¬член можна подати в стандартному вигляді, наприклад: 2ах - За * 5х + 8 = 2аx - 15ах + 8 = -13ax + 8.
Члени многочлена можна записувати в різній послідов¬ності. Здебільшого їх упорядковують за спадними показ¬никами тієї чи іншої змінної. Наприклад, упорядкувавши многочлен 5ах2 + 6х3 - 4а2х + а4 за спадними степенями змінної х, одержимо 6х3 + 5ах2 -4ах + а4 . Найвищий по¬казник степеня змінної х дорівнює трьом, тому такий мно¬гочлен називають многочленом третього степеня віднос¬но х. Його можна впорядкувати і за спадними степенями змінної а: а4 - 4а2х + 5ах2 + 6x3 Це многочлен четвертого степеня відносно змінної а.
Чи задумувалися ви над таким? Чи є многочленами вирази (а + b)с,(abc)? Іноді відповідають на це запи¬тання ствердно, бо, мовляв, згідно з розподільним законом множен¬ня даний вираз тотожно дорівнює двочленові ас + bс, а отже і він є двочленом. Або, наприклад, запис (abc) (він означає трицифрове число, у якому a сотень, b десятків і c одиниць) перетворюється у тричлен: (abc)= 100a+10b+c . Це неправильно. В алгебрі вирази прийнято називати залежно від того, як вони записані, а не від того, як їх можна записати.
Розглянемо приклад. Вираз 8а можна подати у вигляді суми двох, трьох чи будь-якої іншої кількості доданків:
8а = За + 5а, 8а = а + За + 4а, 8а=а+а+а+а+4а.
Якщо, виходячи з цього, вираз 8а називати і одночленом, і дво¬членом, і тричленом тощо, то це буде дуже незручно. Тому в алгебрі домовилися вирази називати так, як вони записані, а не так, як їх мож¬на записати, виконавши ті чи інші тотожні перетворення.
(а + b)с — ні одночлен, ні многочлен. Теж саме можна стверджувати і про запис (abc). А от вираз ∑_0^n▒〖a_i x^i 〗 можна вважати многочленом, бо це скорочений запис многочлена a_0 x^0+a_1 x^1+a_2 x^2+a_3 x^3+a_4 x^4+…+a_n x^n.
ДОДАВАННЯ І ВІДНІМАННЯ МНОГОЧЛЕНІВ
Щоб додати два многочлени, тобто знайти суму многочленів, достатньо сполучити їх знаком «плюс». Наприклад, сумою многочленів а2 + ах + x3 і с2 + сх + х є многочлен а2 + ах + х3 + с2 + сх + х. Якщо в знайденій сумі є подібні члени, їх слід звести. Так само додають три і більше многочленів.
Приклад. Додайте многочлени х2 + 2х + 4, 3х2 - 4 і 3 - 2х. Розв’язання. х2 + 2х + 4 + 3х2 - 4 + 3 - 2х = 4х2 + 3. Додавання многочленів підпорядковується перестав¬ному і сполучному законам: які б не були многочлени А, В і С, завжди А + В = В + А і (А + В) + С = А + (B + С).
Щоб знайти різницю двох многочленів, треба від першо¬го з них відняти другий. Виконуючи таке завдання, після першого многочлена пи¬шуть знак «мінус», а другий беруть у дужки. Розкриваючи дужки, перед якими стоїть знак «мінус», знаки всіх членів, що були в цих дужках, змінюють на протилежні.
Приклад. Знайдіть різницю многочленів аb + с - 4 і 2аb + с - 3. Розв’язання. аb + с - 4- (2 аb + с - 3) = аb + с - 4 - 2аb - с + 3 = -аb - 1.
Отже, і сума, і різниця довільних многочленів — много¬члени.
Хочете знати ще більше?
Якою може бути сума двох двочленів? Вона може мати кілька членів, дорівнювати якому-небудь числу, зокрема й нулю. Додайте, на¬приклад, до двочлена 4с - 5х послідовно двочлени с2 + 1, с2 + 5х, 5х-7, 5х - 4с і переконайтеся в цьому.
Оскільки многочленами вважають і одночлени, і будь-які числа, зокре¬ма й нуль, то сума будь-яких многочленів є многочленом. Тому говорять, що в множині многочленів додавання і віднімання завжди можливе.
Висновки
В алгебрі домовилися вирази називати так, як вони записані, а не так, як їх мож¬на записати, виконавши ті чи інші тотожні перетворення. Тому записи (а+в)с та (авс) ̅ (та інші ) многочленами не вважаються.