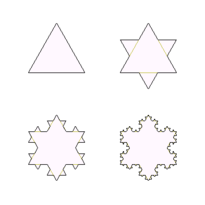
"Класифікація найпоширеніших видів фракталів?"

Зміст

1 Автори проекту
2 Проблемні запитання (запитання для дослідження)
3 Гіпотеза дослідження
4 Мета дослідження
5 Результати дослідження
6 Висновки
7 Корисні ресурси

Автори проекту

Учні 9-А класу КУ СЗОШ № 23, м. Суми

Проблемні запитання (запитання для дослідження)

Що таке фрактал?
Історія виникнення теорії фракталів
Класифікація найпоширеніших видів фракталів

Гіпотеза дослідження

Дослідження фракталів відкриває широкі можливості вивчення оточуючого світу. Вивчивши класифікацію найпоширеніших видів фракталів ми зможемо виконувати наукові дослідження у різних галузях та подивитися на моделювання природніх процесів під різним кутом зору.

Мета дослідження

Вивчення найпоширенішіх видів фракталів. Створення об'єктів, образи яких схожі на природні.

Результати дослідження

Термін фрактал (від лат. fractus - ламаний; англ. fractional - дрібний) уведений у науковий обіг у 1975 році математиком Бенуа Б. Мандельбротом для опису низки об'єктів та явищ, які не мають визначеного лінійного розміру. Б. Б. Мандельброт запропонував найзагальніше означення фрактала ("це певна структура, яка складається з подібних до себе підструктур") та алгоритми побудови різних типів фракталів як нерегулярних і самототожних (самоподібних) структур. Фрактал - це явище, яке існує й декларує себе динамічно, він є процесом. Властивості фракталів як об'єктивного процесу змінюються у межах від чіткої регулярности до хаосу. Поруч з усім можна зробити логічний, хоч і достатньо парадоксальний висновок: фрактальні форми притаманні нескінченній кількости структур та процесів, оскільки, "по суті, Мандельброт відкрив математичний вираз для надзвичайно загальної закономірности, що стосується геометричних властивостей фізичного світу".

Сніжинка Коха є межею нескінченної конструкції, що починається з трикутника та доповнюється рекурсивною заміною кожного сегменту набором із чотирьох сегментів, які утворюють трикутний «виступ». Щоразу, коли додаються нові трикутники (при ітерації), периметр фігури зростає на третину й тому прямує до нескінченності, коли кількість ітерацій прямує до нескінченності. Довжина межі сніжинки Коха, таким чином, є нескінченною, а її площа — скінченною.

Об'єкти, які тепер називаються фракталами, досліджувались задовго до того, як їм було дано таку назву. В етноматематиці, наприклад в роботах Рона Еглаша «Африканські Фрактали», (ISBN 0-8135-2613-2) задокументовано поширені фрактальні геометричні фігури в мистецтві тубільців. В 1525 році німецький митець Альбрехт Дюрер опублікував свою працю Керівництво Художника, один із розділів якої має назву «Черепичні шаблони, утворені пентагонами». Пентагон Дюрера багато в чому є схожим на килим Серпінського, але замість квадратів використовуються п'ятикутники. Джексон Поллок (американський експресіоніст 50-тих років) малював об'єкти, дуже схожі на фрактали. Ідею «рекурсивної самоподібності» було висунено філософом Лейбніцом, який також розробив багато з деталей цієї ідеї. В 1872 Карл Веєрштрас побудував приклад функції з неінтуітивною особливістю, скрізь неперервної, але ніде недиференційовної — графік цієї функції тепер би називався фракталом. В 1904 Хельга Фон Кох, незадоволений занадто абстрактним та аналітичним означенням Веєрштраса, розробив більш геометричне означення схожої функції, яка тепер має назву сніжинки Коха. Ідею самоподібних кривих було далі розвинено Полєм П'єром Леві, який у своїй роботі Криві та поверхні на площині та у просторі, які складаються із частин, схожих на ціле, виданій 1938 року, описав нову фрактальну криву, відому тепер як Крива Леві. Ґеорг Кантор навів приклади підмножин дійсних чисел із незвичними властивостями — ці множини Кантора тепер також визнаються як фрактали. Ітераційні функції на комплексній площині досліджувались в кінці 19 та на початку 20 століття Анрі Пуанкаре, Феліксом Кляйном, П'єром Фату та Ґастоном Жюліа. Проте за браком сучасної комп'ютерної графіки у них забракло засобів відобразити красу багатьох із відкритих ними об'єктів. В 1960-их роках, Бенуа Мандельброт почав дослідження самоподібності в своїх роботах, наприклад Яка довжина узбережжя Британії? Статистична самоподібність та дробова розмірність. Ця доповідь базувалась на ранніх роботах Луі Фрая Річардсона. В 1975 році Мандельброт використав слово фрактал як назву для об'єктів, розмірність Хаусдорфа яких є більшою за топологічну розмірність. Він проілюстрував своє математичне означення захоплюючими зображеннями, зробленими за допомогою комп'ютера. Ці зображення привернули велику увагу; багато з них базувалися на рекурсії, що призвело до появи поширеного розуміння слова фрактал.

Деякі інші приклади фракталів:

Множина Мандельброта, Килим Серпинського

Із застосуванням фракталів Ви можете ознайомитися, переглянувши презентацію "Де ми можемо побачити фрактали у природі?"

Висновки

Наостанок зазначимо, що у ході дослідження гіпотеза підтвердилася. Отже, концепція фракталів стає не тільки частиною "чистої науки", але й елементом загальнолюдської культури. Фрактальна наука ще дуже молода, і їй пророкують велике майбутнє. Краса фракталів далеко не вичерпана і ще подарує людству чимало шедеврів - тих, які радують зір, і тих які дають насолоду розуму.